What is that scarf?
If you meet me in person, you might notice that I’m carrying around one of these knitting projects. Both projects bear patterns that are imbued with deeper mathematical stories.

Rule 110 Scarf
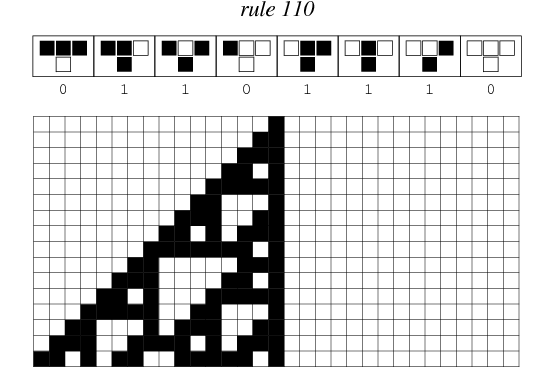
My first knitting project is a scarf that depicts Wolfram’s Rule 110 elementary cellular automaton.
Hang on, what’s an elementary cellular automaton?
Maybe you’ve heard of Conway’s Game of Life? Conway’s Game of Life is a two-dimensional cellular automaton; it features a grid of pixels, and the grid evolves according to a particular ruleset, timestep by timestep.
Wolfram’s elementary cellular automata are similar, but they’re one-dimensional; a single line of pixels evolves according to a particular ruleset, timestep by timestep. Typically, the time dimension is shown going downwards, as in the above depiction of rule 110.
Furthermore, elementary cellular automata are constrained so that each pixel in the next generation can only depend on the three pixels immediately above it.
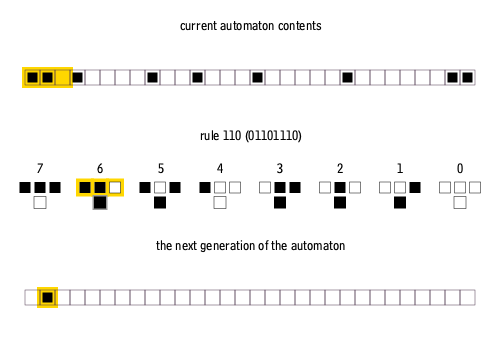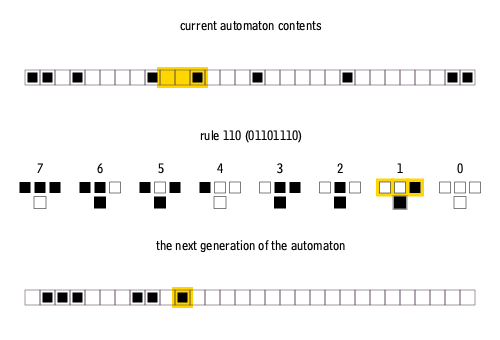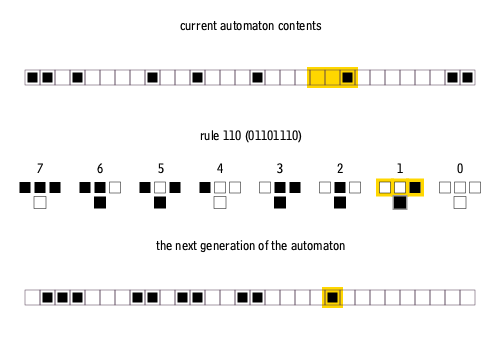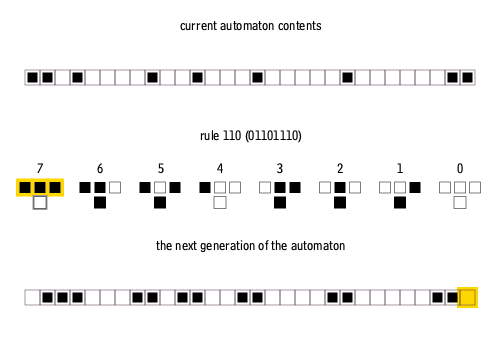
There are many ways to create rules for elementary cellular automata. Each rule is uniquely defined by the set of eight pixels that it prescribes as the descendant for each of the eight possible three-pixel combinations of ancestor pixels. Therefore, there are 2^8 = 256 possible elementary cellular automaton rules, of which rule 110 is merely one.
Why choose Rule 110?

Rule 110 after 250 iterations
It just so happens that Rule 110 is Turing-complete, as proven in Universality in Elementary Cellular Automata (Cook 2004)!
(Conway’s Game of Life, incidentally, is also Turing-complete, as shown by such lovely constructions as Universal Turing Machine in Life or even Life in Life)
The proof is a cute little construction. First, it identifies several gliders which move predictably through a specially-defined “ether” (a repeating background pattern), and then it classifies the ways in which the gliders can collide and interact depending on their spacing at the time of their collision.

Three gliders (image credit)

Two types of collision (image credit)
By carefully handling the ways in which gliders are initialized and are set up to collide, it is possible to carry out enough computation in order to emulate cyclic tag systems, a formalism which was already known to be Turing-complete.
This particular knitting project is close to my heart, as Rule 110’s Turing-completeness gives it a certain numinous beauty and mystery. Why, of Wolfram’s 256 elementary cellular automata, should it be the case that that there is even one that is Turing-complete? Amidst the unruly chaos of Rule 30’s pseudorandom number generation and the ordered austerity of Rule 90’s perfect Sierpinski triangles, what deep mathematical forces conspired to give us this – this simple rule which, by itself alone, is capable of just enough complex behavior to be capable of carrying out computations? It balances on the knife’s edge between the dynamic and the static, exhibiting a kind of critical behavior of the sort that can also be seen in discussions of neuroscience and the physics of phase transitions.
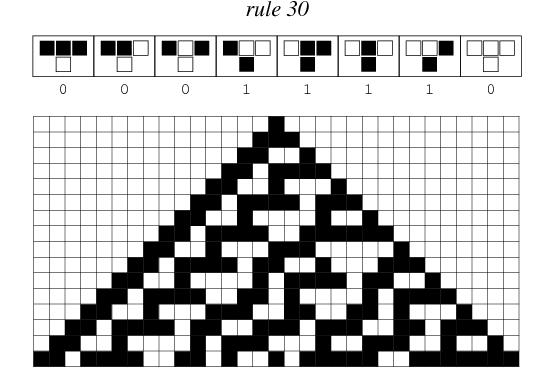
Rule 30, sometimes used as a pseudorandom number generator
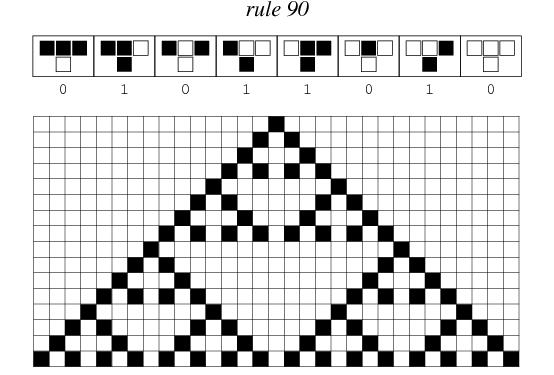
Rule 90, which generates Sierpinski triangles when initialized with a single pixel
The scarf also serves for me as a physical symbol of the following cluster of philosophical problems: What ethics govern the simulation of minds? If I were to create a scarf with a simulation of a mind in a video game environment (such as the one in The Talos Principle), is it at all meaningful – ethically – for me to sit there and knit out the entire scarf so that the simulation’s output is legible to us, or is it equally meaningful for me to merely cast on the start state of the scarf, and note how I might allow the computation to proceed if I were to knit out the entire scarf? If the two situations are the same, is it also equally meaningful for me to merely think about creating the scarf, designing its start state in my head, but never casting it onto physical yarn? And if the full spectrum of situations are not the same, then why?

I used YouTube videos to learn the technique of double-knitting in order to be able to construct a scarf with a two-color pixelated pattern. Due to the double-knitting constraint, the pixels on one side of the scarf are inverted on the other side, so technically it’s a scarf bearing Rule 110 on one side and Rule 193 on the other.
Rule 105 Scarf
Unlike the rule 110 scarf, this knitting project is my current work in progress.
The premise: Let’s say you want to create a Möbius strip scarf… but you also want it to be a cellular automaton.
Simply diving in to knitting any old cellular automaton won’t do, because in order to make it be Möbius, you must flip it around and join it to itself as the end of the process. For example, I clearly cannot do this with my rule 110 scarf. As shown, the final row does not proceed smoothly into the starting row, as would have been required!

What’s more, even deeper than this requirement about the final row’s behavior is the requirement that the whole cellular automaton rule must continue to be the same, even when we flip the scarf around. As we can see in the above example, leftward-leaning white triangles on blue (Rule 110) is a completely different pattern texture from rightward-leaning blue triangles on white (Rule 193).
This imposes the following two constraints on any cellular automaton we choose to Möbiusify:
- The rule must be left-right symmetric.
- The rule must be zero-one symmetric.
Alternatively put, using Wolfram’s terminology, the rule must be equal to its mirrored complement.
This requirement limits us to a small handful of valid rules, many of which are so simple as to be blindingly, boringly unaesthetic. (Rule 51 is one example of a blindingly boring rule, not that I have any problem with stripes.)
I decided to choose Rule 105 for its aesthetics. Rule 150 is another nice one that I considered.
I also needed to choose how to deal with the boundary conditions. I decided to treat the edges as if the scarf wraps around on itself. In a certain sense, this makes it perhaps more like a Klein bottle than a Möbius strip, spiritually if not literally.
Given all of the above parameters, the only thing that remained to do was to find a starting state that produces a pattern that repeats on itself in an interesting, pretty way. Most starting states only repeat on themselves after a small number of timesteps – boring! I wanted to maximize the cycle length of my scarf, for maximum aesthetic appeal.
I sent over all of the above parameters to Anders as a small puzzle, and three lines of Mathematica later, received a characterization of the complete 22-dimensional optimal solution space on scarves of 38 columns, from which I chose the following start state. Using this start state, the pixels at row 511 are exactly what they need to be such that the row at 512 is a left-right-flipped and zero-one-flipped copy of row 1 – the mirrored complement!

Row 1 and the first several rows.
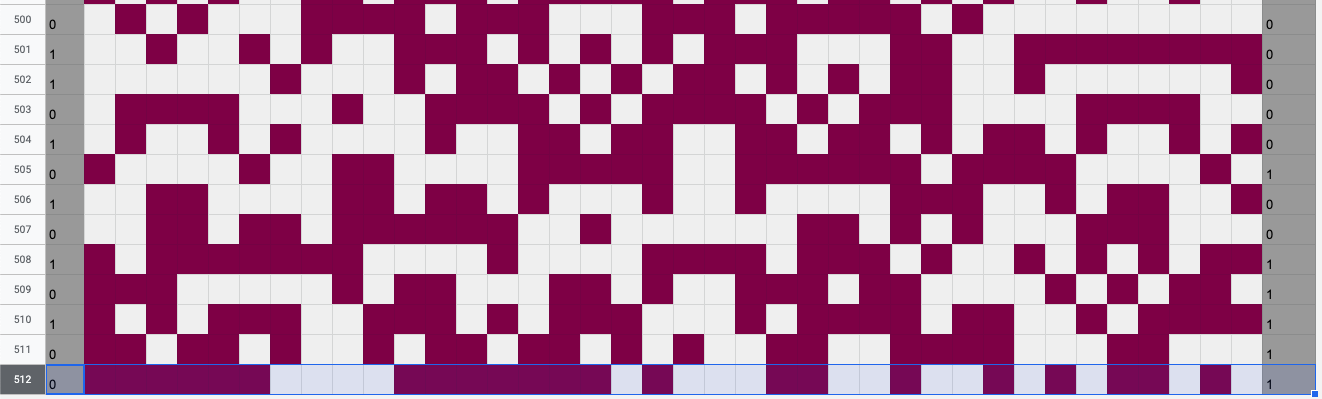
Row 512 is the mirrored complement of row 1.
I’m practicing the provisional cast-on knitting technique in order to make sure that once I reach row 511, I will be able to seamlessly knit the scarf to itself with nobody the wiser about where the scarf ever began or ended. That’s the red yarn in the below picture.
Right now I’m around 30 rows in. It’s going to be a long one!

I was inspired to start knitting by some friends who use knitting as a way to keep their hands busy while still attending to verbal inputs, such as having conversations or listening to others. The knitting projects themselves were inspired by the work of Fabienne Serriere (KnitYak), who creates scarves with cellular automata and other beautiful mathematical patterns using her industrial knitting machine. (She’s even got some of Rule 110 and Rule 105!)
Future work
Once I finish the Möbius strip scarf, the ultimate knitting project for me would be to create another Rule 110 project and have it actually encode a real Turing machine this time, unpacking the lessons from Cook’s proof of Rule 110’s Turing completeness in order to do so. I would pick a small Turing machine, convert it to a universal cyclic tag system using the polynomial reduction of Neary and Woods (2006), and then convert that into a Rule 110 start state.
A Concrete View of Rule 110 Computation (Cook 2009) demonstrates by example how to perform these reductions in order to compile a Turing machine into a Rule 110 cellular automaton. The resulting pattern would be wide enough that it would need be a blanket instead of a scarf!
If I wanted to truly satisfy my artistic preferences over such a project, I’d make sure to pick a Turing machine that’s a nice meaningful one. It’s too bad that A Relatively Small Turing Machine Whose Behavior Is Independent of Set Theory (Aaronson and Yedidia 2016) has 7,918 states, otherwise I would love to encode it!
The best-known five-state Busy Beaver Turing machine might be a nice, simple Turing machine to use for such a project. The best candidate currently known for BB(5) takes 47,176,870 steps before finally halting.

State transitions for a candidate BB(5), as given in Attacking the Busy Beaver 5.

A space-time history of the activity of Rule 110, started at the top with a row of randomly set cells, from Universality in Cellular Automata. Perhaps you see now what I mean by “blanket”.