Hello and welcome to my Coronavirus Genome Walkthrough.

(Hoping someone comes out with that Vaccine Speedrun soon. This boss battle is really shaping up to be an intense one and we’ll need all the artifacts we can get.)

Here, I aim to provide a mechanistic explanation of the SARS-CoV-2 genome’s syntax and semantics. Let’s investigate what the SARS-CoV-2 viral genome actually does as if reading through code like a compiler, from nucleotides to amino acids all the way to proteins. From the four base pairs all the way up to the completed protein-coated virus, what is a virus like this is actually made of on the concrete, physical level?

Understanding a Full System

The underlying purpose of this essay is less about the coronavirus per se and more about how having a small—but functionally complete—piece of viral RNA to analyze gives me a unique opportunity to try to understand a complete self-replicating machine from scratch. This is not a feat that I would have the fortitude to manually replicate with the full human genome, for example—but the coronavirus genome, like the nematode genome, is small enough that we stand a chance at building a complete understanding. The task is perhaps akin to interpretability, but for biological systems instead of artificial neural networks.

As a consequence, this essay is not intended to produce epidemiological conclusions; there are plenty of other sources for that! This essay is about fully understanding a biological system at the chemical and physical level.

Play, Curiosity, and Mechanical Understanding

Throughout this essay, I follow my curiosity in the style of serious play: if I notice I’m confused about something, I look into it and explore it until I’m satisfied that I now understand, and that my understanding is a mechanical understanding. Things are made of stuff! It turns out that we can understand that stuff!

I may skip over some details that were not confusing to me during my own research, but your journey need not be the same as mine. If you’re confused about something while reading this essay, I encourage you to go and look it up! Notice when your curiosity arises; that’s the meditation. It’s always possible to discover the frontier of your own knowledge and to expand it.

This all, at least, has been my intention as I set out to create this piece! As Ken Liu said of his philosophy while translating The Three-Body Problem, “I may not have succeeded, but these were the standards I had in mind as I set about my task.”

Part 1, here, covers just the genome and its translation to proteins. I hope to also write a Part 2 which would cover the structure and function of those proteins, their protein-protein interactions, and the full viral life cycle.

Let’s get started.

Viruses

As a reminder, SARS-CoV-2 is a positive-sense single-stranded RNA virus.

Positive-sense single-stranded RNA virus - Wikipedia

en.wikipedia.org

What does this mean we can expect?

1. Single-stranded: Its genome is a single strand of RNA (ssRNA).
2. Positive-sense: That single strand of RNA can be immediately translated into protein by the ribosomes of the cell it infects.

From this we can also infer that one of the proteins the virus encodes for must be RNA-dependent RNA polymerase (RdRP), a protein which synthesizes new RNA given an RNA template. That’s right: RNA → RNA. However, according to the central dogma of molecular biology, isn’t RNA → RNA an unconscionable heresy? Correspondingly, RdRP is not naturally found in cells! All known positive-sense ssRNA viruses therefore must encode RdRP in order to successfully commit this heresy.

RNA-dependent RNA polymerase - Wikipedia

en.wikipedia.org

…Wait a minute, the phrase “positive-sense ssRNA virus” implies the existence of negative-sense viruses. If those don’t encode their proteins directly, how can they possibly work?

Positive sense and negative sense

Negative-sense ssRNA viruses also exist! Influenza, Ebola, and measles are examples.

Negative-sense single-stranded RNA virus - Wikipedia

en.wikipedia.org

The inner contents of negative-sense ssRNA viruses consist not of an RNA genome but of a ribonucleoprotein, which incorporates both an RNA genome as well as a cohort of viral proteins capable of replicating RNA. Unlike positive-sense ssRNA viruses, negative-sense ssRNA viruses must travel with a working copy of their RNA-replicating proteins. This ribonucleoprotein has enzymatic activity!

RdRP as drug target

Since RdRP has (as far as I know) no legitimate purpose in human cells and is not naturally coded by them, might it offer a potential target for novel antiviral drugs?

Velkov et al. 2014 explores RdRP as a drug target for antivirals against the Hendra virus, a negative-sense ssRNA virus, though I am unable to find the full text.

This review examines the current knowledge based on the multi-domain architecture of the Hendra RdRP and highlights which essential domain functions represent tangible targets for drug development against this deadly disease.

There must be some reason that developing antivirals against this protein is technically (or socially) complicated, or I’d have expected us to do it by now – there are a lot of RNA viruses that this drug target could theoretically hit. Flagging this discrepancy for further research.¹

The full genome

Back to SARS-CoV-2! First, let’s get us a genome. Obviously this virus has seen some mutations as it’s spread around, as you can explore at NextStrain, so we’ve technically got choices as to which one to analyze. For this thread I’ll just stick to analyzing one version of the genome: Wuhan-Hu-1.

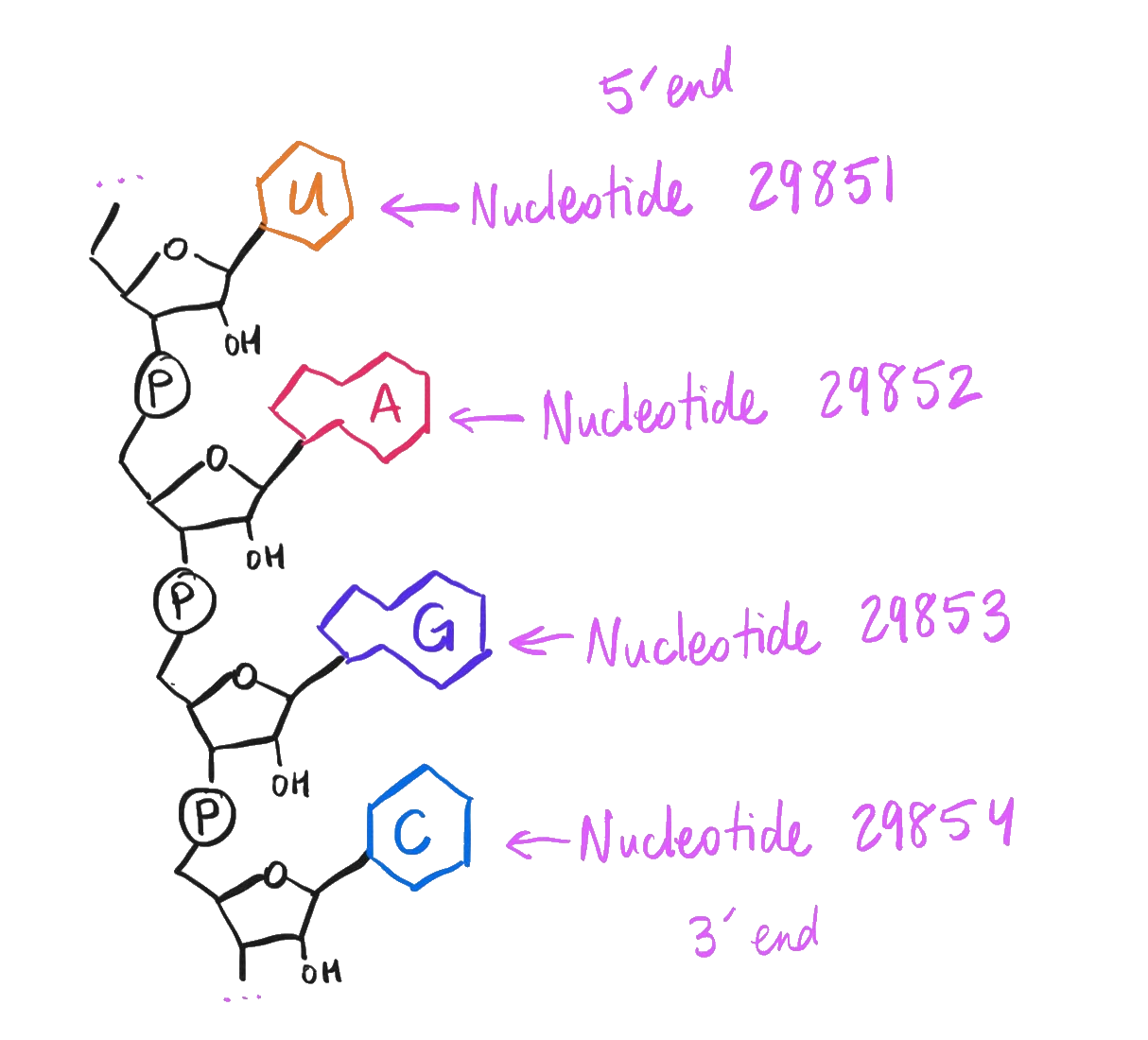
As a reminder, each A, G, C, and T in a genome is one of the four nucleotides: adenine, guanine, cytosine, and thymine. There are actually plenty of ways to engineer different unnatural base pair systems by adding artificial nucleotides, and these can even be integrated into transcription and translation, but for whatever reason, these four and not others are what life ultimately ended up with.

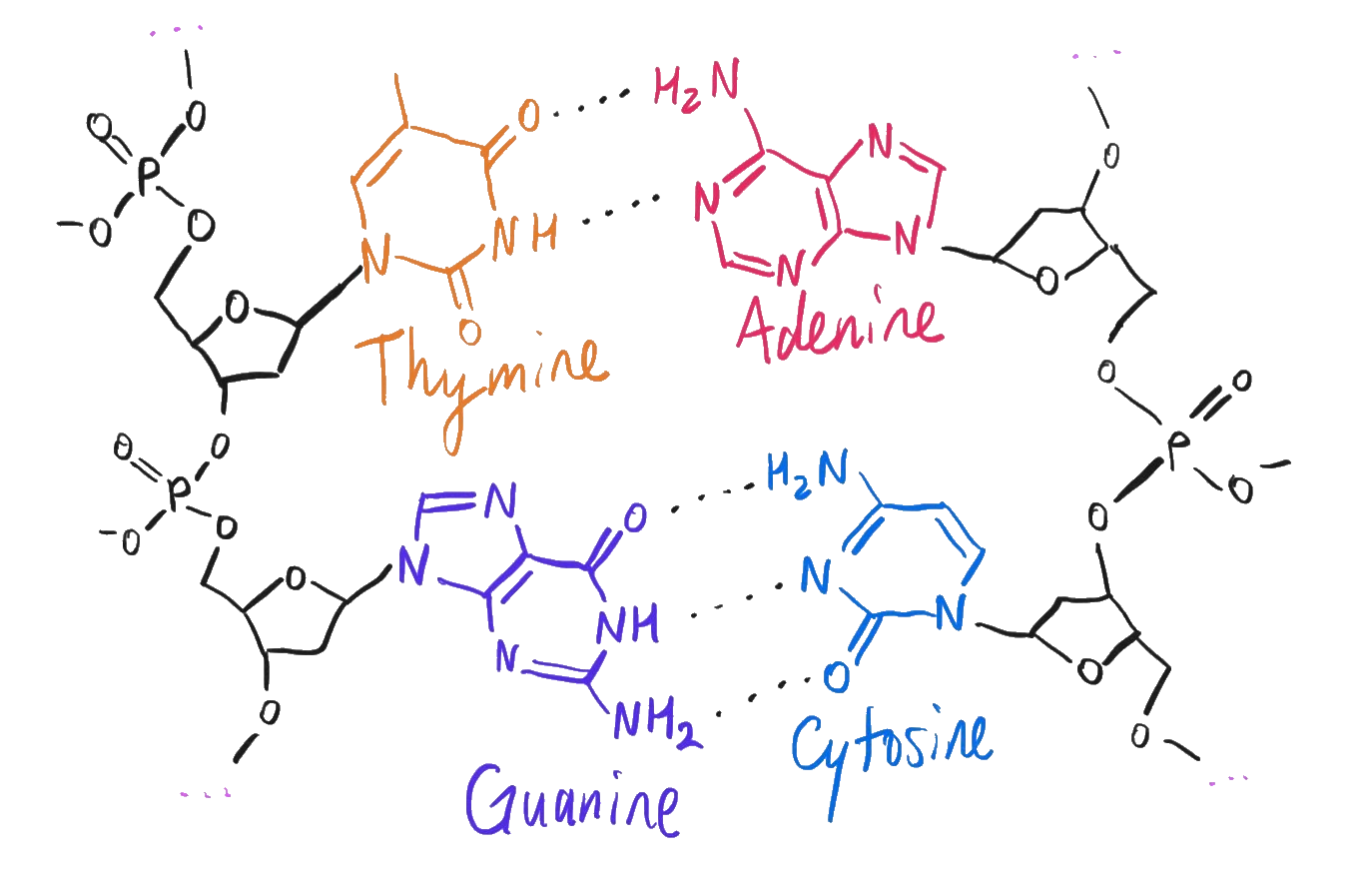
The four nucleotides in DNA.

The genome of Wuhan-Hu-1 is available from NCBI GenBank. Since SARS-CoV-2 is an RNA virus, each T in this string technically represents a U, for uracil, RNA’s information-equivalent of thymine. The genome sequence is therefore:

1     AUUAAAGGUU UAUACCUUCC CAGGUAACAA ACCAACCAAC UUUCGAUCUC UUGUAGAUCU
61    GUUCUCUAAA CGAACUUUAA AAUCUGUGUG GCUGUCACUC GGCUGCAUGC UUAGUGCACU
121   CACGCAGUAU AAUUAAUAAC UAAUUACUGU CGUUGACAGG ACACGAGUAA CUCGUCUAUC

...

29761 ACAGUGAACA AUGCUAGGGA GAGCUGCCUA UAUGGAAGAG CCCUAAUGUG UAAAAUUAAU
29821 UUUAGUAGUG CUAUCCCCAU GUGAUUUUAA UAGCUUCUUA GGAGAAUGAC AAAAAAAAAA
29881 AAAAAAAAAA AAAAAAAAAA AAA

Follow along with the genome »

That’s 29,903 nucleotides. Since there are only four possible nucleotides, we can estimate the information compression value of each nucleotide at approximately 2 bits; the virus’s genome therefore requires only 7.5 kilobytes to store. That’s roughly as much data, byte for byte, as there are characters in this essay up to this point!

Lay out those 29,903 nucleobases along a ribose-phosphate backbone, reading them left to right from the 5’ end to the 3’ end, and bam – if that single molecule* were teleported into a cell, that’s 100% chemically sufficient** to infect a person with the plague du jour.

*plus the 5’ cap, discussed below

**modulo viral load effects??

How to interpret the Wuhan-Hu-1 genome as a complete molecule.

Poly-A tail

First question, and perhaps the most obvious one to the naked eye – what’s with all the AAAAA at the end of the viral genome?

29821 ...                                                ... AAAAAAAAAA
29881 AAAAAAAAAA AAAAAAAAAA AAA

Follow along with the genome »

It’s… yelling at us? Is it… suffering? Should we help?

Simple: It’s a 3’ poly-A tail! This long tail of adenosine monomers is extremely common in both our own cells and in RNA viruses.

Our own messenger RNA (mRNA) has a poly-A tail when it’s freshly produced in the nucleus so as to slow its degradation by the cell, allowing it to last long enough to be transcribed into protein. Naturally, if you’re a positive-strand RNA virus, you’re also going to want to last long enough to be transcribed into protein – so, you need the same feature, yourself.

Genome 0.11% explained. So far so good!

5’ cap

While we’re discussing chemical features of mRNA, note that the viral genome presumably must also have a 5’ cap – an extra 7-methylguanosine at the 5’ end of its RNA strand – just like mRNAs do.

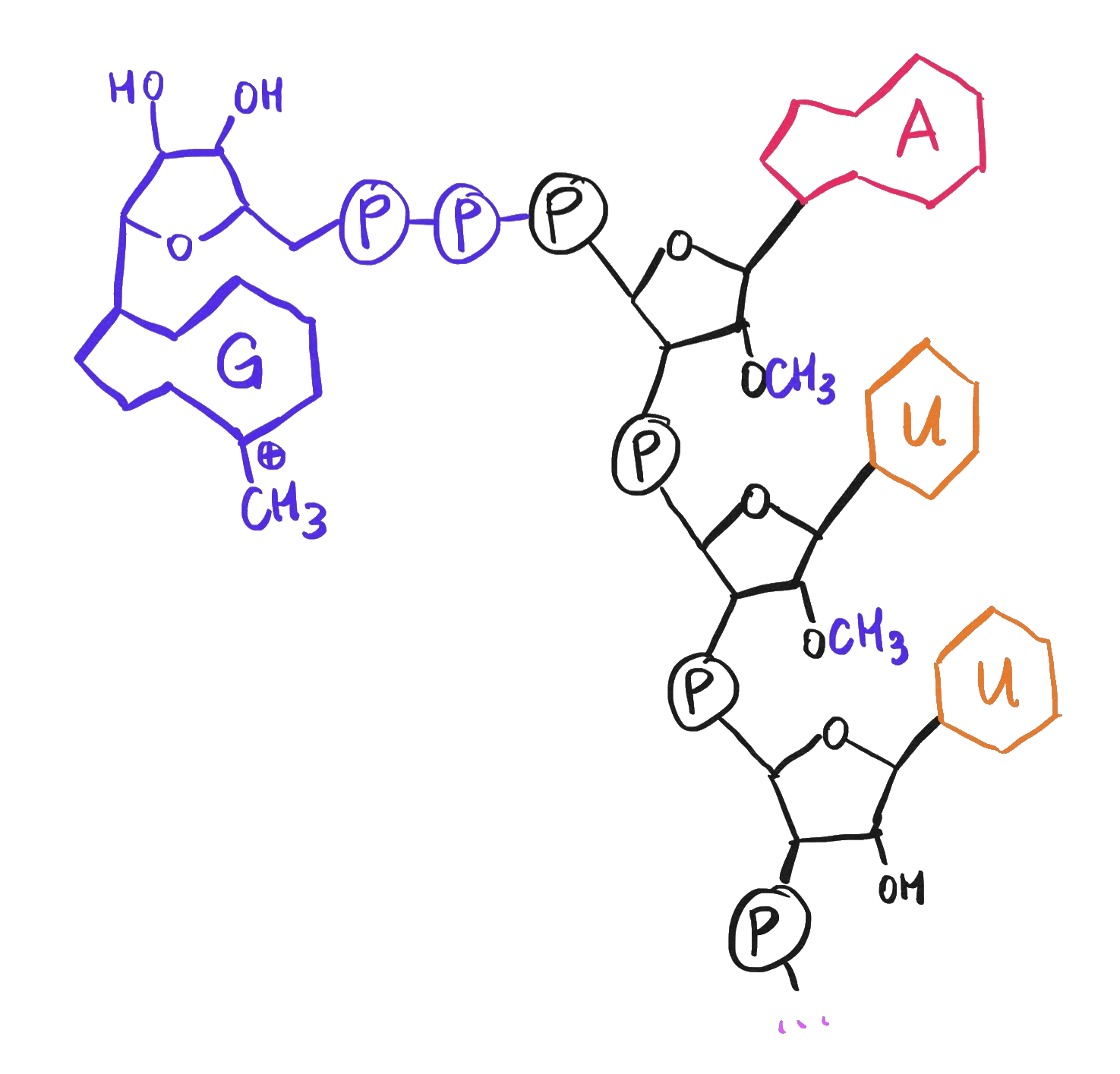
A 5' cap, consisting of a 7-methylguanosine as well as methylation of the first two ribose sugars.

The cap is not directly shown in the viral genome sequence or mentioned in NCBI GenBank, but it is referenced in multiple papers discussing coronaviral genomes:

Since 2003, the outbreak of severe acute respiratory syndrome coronavirus has drawn increased attention and stimulated numerous studies on the molecular virology of coronaviruses. Here, we review the current understanding of the mechanisms adopted by coronaviruses to produce the 5′-cap structure and methylation modification of viral genomic RNAs.

Molecular mechanisms of coronavirus RNA capping and methylation

The 5′-cap structures of eukaryotic mRNAs are important for RNA stability, pre-mRNA splicing, mRNA export, and protein translation. Many viruses have evolved mechanisms for generating their own cap structures with methylation at the N7 position of the capped guanine and the ribose 2′-Oposition of the first nucleotide, which help viral RNAs escape recognition by the host innate immune system. The RNA genomes of coronavirus were identified to have 5′-caps in the early 1980s. However, for decades the RNA capping mechanisms of coronaviruses remained unknown. Since 2003, the outbreak of severe acute respiratory syndrome coronavirus has drawn increased attention and stimulated numerous studies on the molecular virology of coronaviruses. Here, we review the current understanding of the mechanisms adopted by coronaviruses to produce the 5′-cap structure and methylation modification of viral genomic RNAs.

link.springer.com

Coronaviruses possess a cap structure at the 5′ ends of viral genomic RNA and subgenomic RNAs, which is generated through consecutive methylations by virally encoded guanine-N7-methyltransferase (N7-MTase) and 2′-O-methyltransferase (2′-O-MTase). The coronaviral N7-MTase is unique for its physical linkage with an exoribonuclease (ExoN) harbored in nonstructural protein 14 (nsp14) of coronaviruses.

Structure-Function Analysis of Severe Acute Respiratory Syndrome Coronavirus RNA Cap Guanine-N7-Methyltransferase

Coronaviruses possess a cap structure at the 5′ ends of viral genomic RNA and subgenomic RNAs, which is generated through consecutive methylations by virally encoded guanine-N7-methyltransferase (N7-MTase) and 2′-O-methyltransferase (2′-O-MTase). ...

www.ncbi.nlm.nih.gov

Here, we have reconstituted complete SARS-CoV mRNA cap methylation in vitro.

In Vitro Reconstitution of SARS-Coronavirus mRNA Cap Methylation

SARS-coronavirus (SARS-CoV) genome expression depends on the synthesis of a set of mRNAs, which presumably are capped at their 5′ end and direct the synthesis of all viral proteins in the infected cell. Sixteen viral non-structural proteins (nsp1 ...

www.ncbi.nlm.nih.gov

Like the poly-A tail, the 5’ cap helps the genome to be recognized and translated by ribosomes rather than destroyed by the cell’s immune response.

How does the virus even ensure that it receives a 5’ cap and a poly-A tail, not to mention its outer coat? Hopefully these questions will be resolved by our review of its genes… let’s move on to look at those!

Translation

Per the “Features” section of the genome, again from NCBI GenBank, here are the identifiable genes in this genome, in order:

1. Orf1ab (for orf1ab polyprotein)
2. S (for surface glycoprotein)
3. Orf3a (for orf3a protein)
4. E (for envelope protein)
5. M (for membrane glycoprotein)
6. Orf6 (for orf6 protein)
7. Orf7a (for orf7a protein)
8. Orf8 (for orf8 protein)
9. N (for nucleocapsid phosphoprotein)
10. Orf10 (for orf10 protein)

Let’s understand how these genes get translated into proteins.

Translation of Orf1ab

This is the first gene in the genome and it is also by far the longest, weighing in at 7,096 amino acids:

1    MESLVPGFNE KTHVQLSLPV LQVRDVLVRG FGDSVEEVLS EARQHLKDGT CGLVEVEKGV
61   LPQLEQPYVF IKRSDARTAP HGHVMVELVA ELEGIQYGRS GETLGVLVPH VGEIPVAYRK
121  VLLRKNGNKG AGGHSYGADL KSFDLGDELG TDPYEDFQEN WNTKHSSGVT RELMRELNGG

...

6961 LGGSVAIKIT EHSWNADLYK LMGHFAWWTA FVTNVNASSS EAFLIGCNYL GKPREQIDGY
7021 VMHANYIFWR NTNPIQLSSY SLFDMSKFPL KLRGTAVMSL KEGQINDMIL SLLSKGRLII
7081 RENNRVVISS DVLVNN

These letters are single-letter amino acid abbreviations.

It is quite long: this virus has 10 genes, and this single gene represents 71.2% of the viral genome.² More on this polypeptide’s structure and function later, but first: how do the underlying nucleotides of the Orf1ab gene produce these particular amino acids?

A thermodynamic surprise: Ribosomal frameshift

The Orf1ab gene spans the range from nucleotide 266 to nucleotide 21,555, inclusive. Nucleotides in this GenBank data are unfortunately 1-indexed, not 0-indexed.

We can see at nucleotide 266 the signature AUG of a start codon, and at nucleotide 21,553 the UAA of an ochre stop codon. So far so good!

241   ...                     ...AUGGA GAGCCUUGUC CCUGGUUUCA ACGAGAAAAC
301   ACACGUCCAA CUCAGUUUGC CUGUUUUACA GGUUCGCGAC GUGCUCGUAC GUGGCUUUGG
361   AGACUCCGUG GAGGAGGUCU UAUCAGAGGC ACGUCAACAU CUUAAAGAUG GCACUUGUGG

...

21481 CUUAGUAAAG GUAGACUUAU AAUUAGAGAA AACAACAGAG UUGUUAUUUC UAGUGAUGUU
21541 CUUGUUAACA ACUAA...                                           ...

Follow along with the genome »

However, confusingly, the length of this coding region is 21,555 - 265 = 21,290, which is not divisible by 3. Usually, 3 nucleotides = 1 amino acid, so a gene’s length is typically divisible by 3. What’s going on?

Note that in the GenBank data the gene is tagged ribosomal_slippage. Also note that in GenBank the gene’s region is notated as join(266..13468,13468..21555) instead of just 266..21555.

After some research, the answer here is that nucleotide 13,468 is actually used twice, thanks to a -1 ribosomal frameshift, a fascinating thermodynamic-biochemical quirk of certain viral genomes!

Per this article on ribosomal frameshifting in viruses:

Programmed ribosomal frameshifting is an alternate mechanism of translation to merge proteins encoded by two overlapping open reading frames. The frameshift occurs at low frequency and consists of ribosomes slipping by one base in either the 5’(-1) or 3’(+1) directions during translation. Some viruses contains both a +1 and a -1 ribosomal frameshift. […]

All cis-acting frameshift signals encoded in mRNAs are minimally composed of two functional elements: a heptanucleotide “slippery sequence” conforming to the general form XXXYYYZ, followed by an RNA structural element, usually an H-type RNA pseudoknot, positioned an optimal number of nucleotides (5 to 9) downstream.

If we look around nucleotide 13,468, we do in fact find the heptanucleotide “slippery sequence” responsible: it’s UUUAAAC. That C is nucleotide 13,468 and it ends up getting transcribed twice.

13441 GUCAGCUGAU GCACAAUCGU UUUUAAACGG GUUUGCGGUG UAAGUGCAGC CCGUCUUACA

Follow along with the genome »

This frameshift gives us a total length of 21,291 nucleotides. Subtract 3 for the stop codon and then divide by 3, and we get a number which matches the reported protein sequence’s length: 7,096 amino acids. Hooray!

So, the math checks out. We now know what ribosomal_slippage and join(266..13468,13468..21555) mean, and we know how these 21,290 nucleotides become 7,096 amino acids. However, I still have two questions:

1. What??
2. How does ribosomal frameshifting even work??

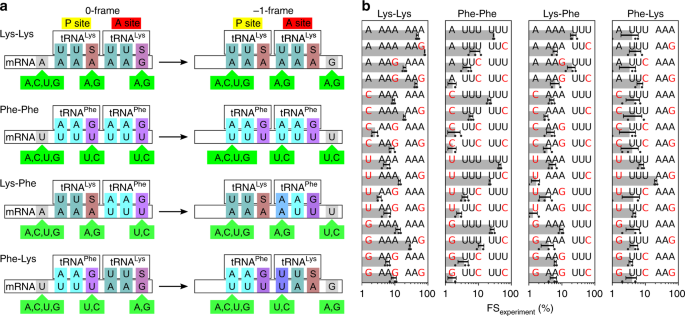
Ribosomal frameshifting at the molecular level

Thermodynamic control of -1 programmed ribosomal frameshifting (Bock et al. 2019) explores how ribosomal frameshifting happens by performing free-energy molecular dynamics simulations. This paper also explains the structure and function of that heptanucleotide slippery sequence, stating:

Spontaneous ribosome slippage is a rare event that occurs, on average, once in 10⁴–10⁵ codons. This low spontaneous frameshifting increases dramatically on particular mRNAs that contain sequences for programmed ribosomal frameshifting (PRF). PRF requires a slippery sequence, which usually comprises a X XXY YYZ heptamer, where XXX and YYY are triplets of identical bases and Z is any nucleotide, which allows for cognate pairing of the P-site and A-site tRNAs in the 0-frame and −1-frame. The nature of the tRNAs bound to the slippery site codons is critical, including the modifications of nucleotides in the anticodon loop (i.e., at positions 34 and 37 of the tRNA).

Thermodynamic control of −1 programmed ribosomal frameshifting

Programmed ribosomal frameshifting (PRF) is an alternative translation strategy that causes controlled slippage of the ribosome along the mRNA, changing the sequence of the synthesized protein. Here the authors provide a thermodynamic framework that explains how mRNA sequence determines the efficiency of frameshifting.

www.nature.com

This paper goes on to analyze several heptanucleotide slippery sequences, drawing examples from the E. coli dnaX gene and explaining their thermodynamic characteristics. Per their breakdown, each example sequence depends on one or more of the following wobble pairings:

• The U·G wobble pair. Per Varani and McClain 2000, the U·G wobble pair “has comparable thermodynamic stability to Watson–Crick base pairs and is nearly isomorphic to them.”
• A·A and U·U mismatches.
• G·S and A·S pairs. Per Bock et al. 2019, E. coli “has a single tRNA^Lys isoacceptor (anticodon ^3’UUS^5’) for decoding the two Lys codons, AAG and AAA,” where “S denotes the modified nucleotide mnm5s2U.”

For example, one of the heptanucleotide slippery sequences explained in Bock et al. is the heptanucleotide sequence UUUUAAG. When the ribosome reads this sequence, it initially parses it as ..U UUU^Phe AAG^Lys, but then jolts -1 backwards into the ... UUU^Phe UAA^Lys reading frame. Despite normally being translated as a stop codon, that second UAA retains its attached tRNA^Lys via the combination of a U·U mismatch and an A·S pair.

The UUUUAAG slippery sequence.

Unfortunately, UUUUAAG isn’t the sequence we’re interested in if we want to understand SARS-CoV-2! We need our particular heptanucleotide slippery sequence of interest, UUUAAAC, and despite this paper’s thoroughness and usefulness, none of its examples involve it. How can we be sure that UUUAAAC has the thermodynamic properties that it needs in order for SARS-CoV-2 to be able to produce a protein here?

After some investigation, I finally stumbled upon Mutational Analysis of the “Slippery-sequence” Component of a Coronavirus Ribosomal Frameshifting Signal (Brierley, Jenner, and Inglis 1992), a research paper which covers exactly this same heptanucleotide sequence (and in the context of coronaviruses, too), and even gives a helpful diagram!

Mutational analysis of the “slippery-sequence” component of a coronavirus ribosomal frameshifting signal

The ribosomal frameshift signal in the genomic RNA of the coronavirus IBV is composed of two elements, a heptanucleotide “slippery-sequence” and a dow…

www.sciencedirect.com

The UUUAAAC slippery sequence.

The paper performs some experiments and confirms how the UUUAAAC slippery sequence works:

1. First, a tRNA^Leu and a tRNA^Asn bind to the UUA and AAC.
2. After a -1 frameshift, those two tRNAs are now wobble-paired to UUU (with a U·U mismatch) and AAA (with an A·G mismatch³).
3. Translation then proceeds as normal from there, with the next codon producing a tRNA^Arg.

I’m still a little weirded out by ribosomal frameshift, but satisfied.

Partial translation of Orf1ab

One last detail while we’re discussing the gene Orf1ab. Numerous papers I’ve read so far seem to allude to the fact that Orf1ab actually produces two protein products: one, its complete protein product (named pp1ab), and another, a partial translation (named pp1a) due to the ribosome falling off at the ribosomal frameshift instead of undergoing a frameshift event. That first half of the sequence itself can be called the gene Orf1a.

For example, from Graham et al. 2008 on the SARS coronavirus:

Translation of ORF1a results in a theoretical polyprotein of ∼500 kDa, while translation of ORF1ab results an ∼800 kDa polyprotein.

The ORF 1a and 1ab polyproteins are not detected during infection, since they are most likely processed co- and post-translationally into intermediate and mature proteins by proteinase activities in the nascent polyproteins.

Both of these genes produce polyproteins that actually get chopped up into smaller proteins before going on to carry out their function, so the possibility of premature termination of pp1a ends up being of little consequence except inasmuch as it partially reduces translation of pp1ab.

Translation of all the other genes

This concludes our analysis of the translation of the Orf1ab gene. Genome 71.31% explained so far!

In comparison, the remaining nine genes are fairly uneventful. They all start with a start codon (AUG), end with a stop codon (UAA, UGA, or UAG), and don’t try to do anything tricky in between.

By their powers combined, that explains 97.53% of the genome. If you take a look at the rest, you’ll see that there isn’t all that much left that’s not accounted for. With the two untranslated regions – there’s the 5’ UTR weighing in at 265 base pairs, and there’s the 3’ UTR (which includes the poly-A tail) weighing in at 229 base pairs. That covers 99.07% of the genome! The remaining 277 base pairs are scattered in the space between the ten genes.

I now feel basically confident that I know what the nucleotides get translated to!

Secondary structure

No discussion of the structure and function of a long, single-stranded piece of RNA is complete without a discussion on secondary structure.

Yes, RNA has secondary structure too – it’s not just for proteins! Just like double-helical DNA binds one strand to another, a single strand of RNA can bind to itself when regions have sufficiently complementary nucleotides, forming stems, hairloops, and yet more complex 3D structures.

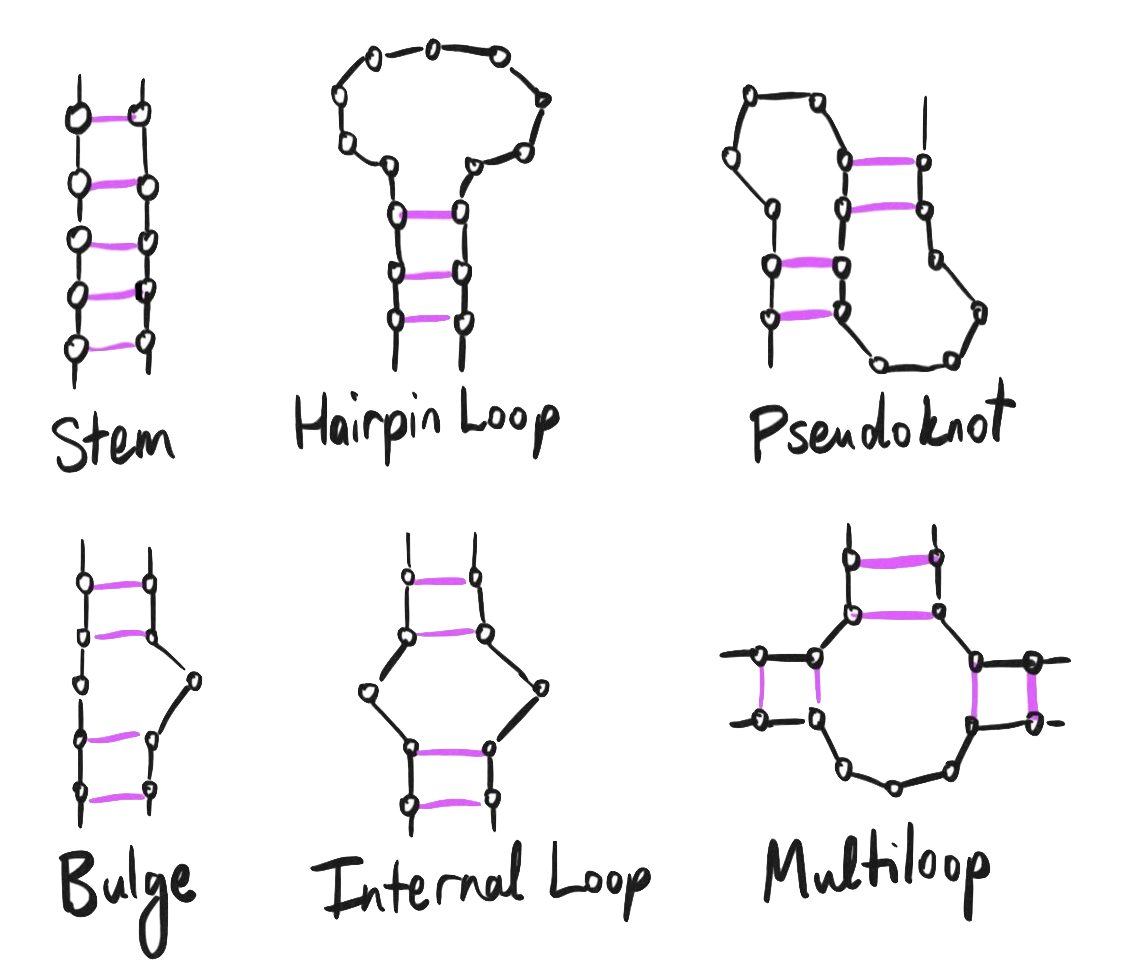
The pseudoknot may sound familiar – it’s mentioned back in our discussion on ribosomal frameshifting:

All cis-acting frameshift signals encoded in mRNAs are minimally composed of two functional elements: a heptanucleotide “slippery sequence” conforming to the general form XXXYYYZ, followed by an RNA structural element, usually an H-type RNA pseudoknot, positioned an optimal number of nucleotides (5 to 9) downstream.

One of the more complex examples of RNA secondary structure, the pseudoknot was first discovered in the turnip yellow mosaic virus, which is itself another single-stranded positive-sense RNA virus just like the coronavirus.

Pseudoknot - Wikipedia

en.wikipedia.org

What’s an H-type RNA pseudoknot, though? According to Cao and Chen 2009,

An H-type pseudoknot is formed by base-pairing between a hairpin loop and the single-stranded region of the hairpin. The structure consists of two helix stems and two loops as well as a possible third loop/junction that connects the two helix stems.

Perhaps we can determine the secondary structure of the SARS-CoV-2 genome, or if not, at least determine the secondary structure for the pseudoknot, as that part serves an important regulatory function.

As we know from our study of ribosomal frameshifting, the pseudoknot should occur around 5 to 9 nucleotides downstream of the slippery sequence. Here’s a snippet of the surrounding genome sequence again:

13441                 ...GU UUUUAAACGG GUUUGCGGUG UAAGUGCAGC CCGUCUUACA
13501 CCGUGCGGCA CAGGCACUAG UACUGAUGUC GUAUACAGGG CUUUUG...

Follow along with the genome »

For RNAs shorter than 4000 nucleotides, there exist some online tools such as RNAfold that can make predictions about the secondary structure of arbitrary RNAs; however, I’m unable to find any that can handle our 29,903-nucleotide minor behemoth of an RNA. So, that leaves me with searching through the existing literature to see what results exist for this particular big long RNA.

Luckily, RNA Genome Conservation and Secondary Structure in SARS-CoV-2 and SARS-Related Viruses (Rangan et al. 2020) gives an overview of some of the virus’s secondary structures, including the pseudoknot, as well as a thoughtful analysis of which structural elements have remained conserved as viruses in this family have evolved!

RNA genome conservation and secondary structure in SARS-CoV-2 and SARS-related viruses

As the COVID-19 outbreak spreads, there is a growing need for a compilation of conserved RNA genome regions in the SARS-CoV-2 virus along with their structural propensities to guide development of antivirals and diagnostics. Using sequence alignments ...

www.ncbi.nlm.nih.gov

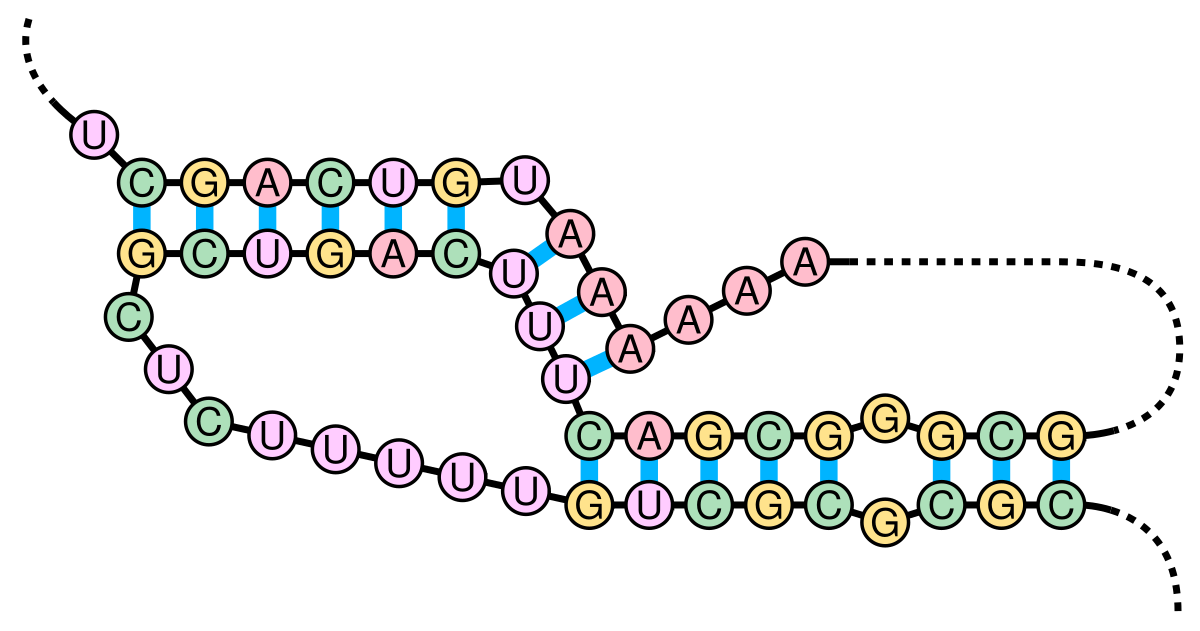
As depicted in that paper’s figure 4, here is how the region near the slippery sequence winds itself into an H-type pseudoknot:

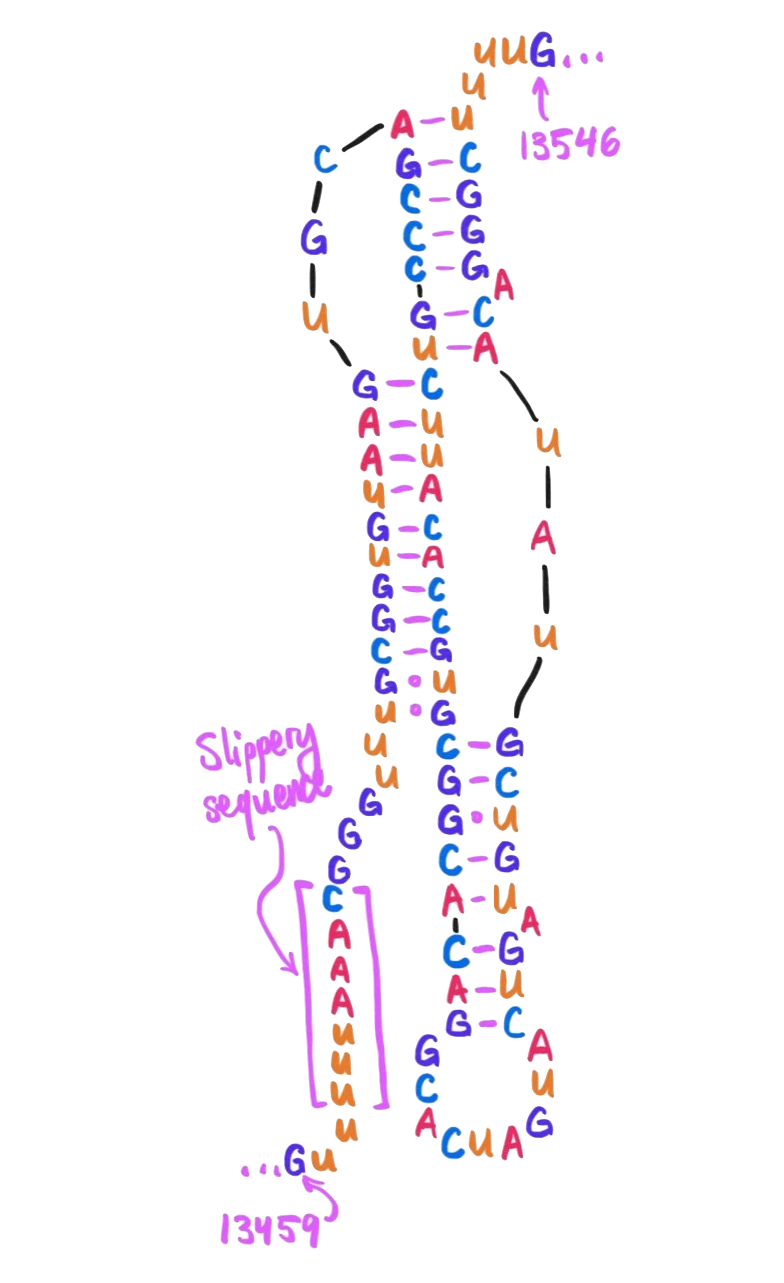
Starting 6 nucleotides after the heptanucleotide slippery sequence, nucleotides 13474 through 13542 together form a pseudoknot. (Here drawn schematically in 2D – in real life they wouldn't be so stretched out!)

Note the presence here of a few U·G wobble pairs, as mentioned in our earlier discussion on wobble pairings!

We can view this pseudoknot in 3D by converting the above secondary structure into dot-bracket notation, passing it into RNAComposer in order to extract a predicted 3D folding as a PDB file, and finally passing that into Web 3DNA to render a 3D image.

GUUUUUAAACGGGUUUGCGGUGUAAGUGCAGCCCGUCUUACACCGUGCGGCACAGGCACUAGUACUGAUGUCGUAUACAGGGCUUUUG
...............(((((((((((...[[[[[[[)))))))))))[[[[[[[[.........]]].]]]]]...]].]]]]]....

The pseudoknot in dot-bracket notation.

The pseudoknot, rendered in 3D.

For more information on secondary structure and how it can affect the life cycle and transmissibility of RNA viruses, as well as details about how secondary structure can be elucidated, I also recommend:

• RNA Structure—A Neglected Puppet Master for the Evolution of Virus and Host Immunity (Smyth et al. 2018)
• Viral RNAs Are Unusually Compact (Gopal et al. 2014)
• Visualizing the global secondary structure of a viral RNA genome with cryo-electron microscopy (Garmann et al. 2015)
• The influence of viral RNA secondary structure on interactions with innate host cell defences (Witteveldt et al. 2014)

Shoutouts

Thanks to Laura Vaughan for a thoughtful review of this piece and for help with RNA 3D structure visualization!

Shoutout also to Nabeel Qureshi who has worked on a similar endeavor, writing up an executable iPython notebook for understanding the full coronavirus genome.

As fate would have it, I know Ramya Rangan from our time as students of Jean Yang! It was really exciting to organically stumble upon a former colleague’s recent work, and especially to have so many of my questions about coronaviral secondary structure just answered immediately by that work.

Next time: Protein is great!

That’s all for now! Stay tuned for part 2, A Mechanist’s Guide to the Coronavirus Proteome.

Footnotes

If you meet me in person, you might notice that I’m carrying around one of these knitting projects. Both projects bear patterns that are imbued with deeper mathematical stories.

Rule 110 Scarf

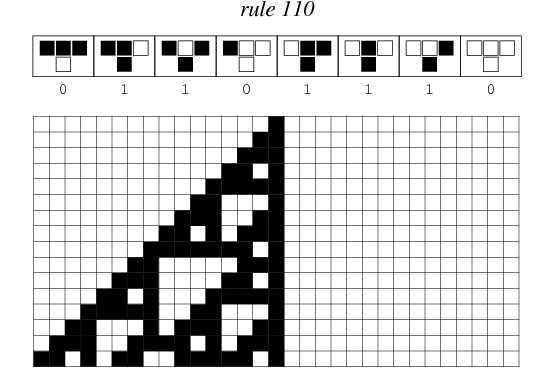
My first knitting project is a scarf that depicts Wolfram’s Rule 110 elementary cellular automaton.

Hang on, what’s an elementary cellular automaton?

Maybe you’ve heard of Conway’s Game of Life? Conway’s Game of Life is a two-dimensional cellular automaton; it features a grid of pixels, and the grid evolves according to a particular ruleset, timestep by timestep.

Wolfram’s elementary cellular automata are similar, but they’re one-dimensional; a single line of pixels evolves according to a particular ruleset, timestep by timestep. Typically, the time dimension is shown going downwards, as in the above depiction of rule 110.

Furthermore, elementary cellular automata are constrained so that each pixel in the next generation can only depend on the three pixels immediately above it.

(image credit)

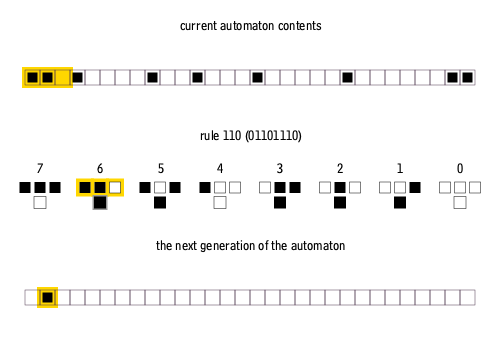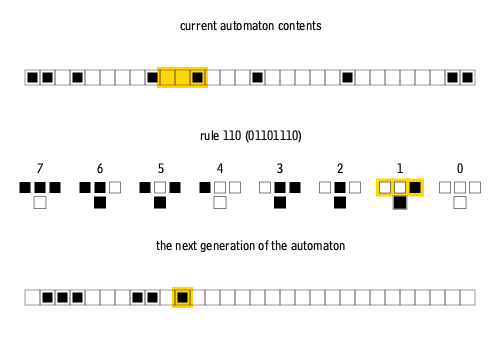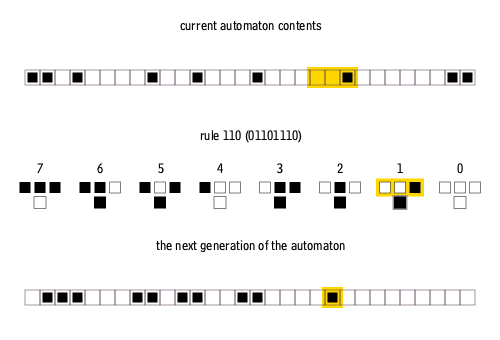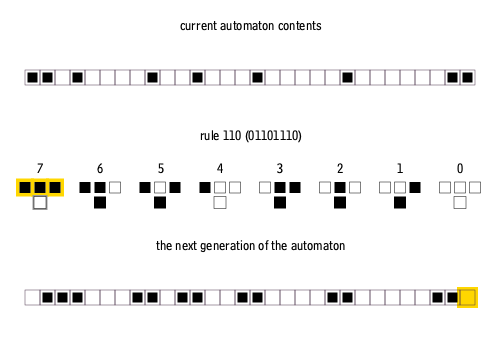
There are many ways to create rules for elementary cellular automata. Each rule is uniquely defined by the set of eight pixels that it prescribes as the descendant for each of the eight possible three-pixel combinations of ancestor pixels. Therefore, there are 2^8 = 256 possible elementary cellular automaton rules, of which rule 110 is merely one.

Why choose Rule 110?

Rule 110 after 250 iterations

It just so happens that Rule 110 is Turing-complete, as proven in Universality in Elementary Cellular Automata (Cook 2004)!

(Conway’s Game of Life, incidentally, is also Turing-complete, as shown by such lovely constructions as Universal Turing Machine in Life or even Life in Life)

The proof is a cute little construction. First, it identifies several gliders which move predictably through a specially-defined “ether” (a repeating background pattern), and then it classifies the ways in which the gliders can collide and interact depending on their spacing at the time of their collision.

Three gliders (image credit)

Two types of collision (image credit)

By carefully handling the ways in which gliders are initialized and are set up to collide, it is possible to carry out enough computation in order to emulate cyclic tag systems, a formalism which was already known to be Turing-complete.

This particular knitting project is close to my heart, as Rule 110’s Turing-completeness gives it a certain numinous beauty and mystery. Why, of Wolfram’s 256 elementary cellular automata, should it be the case that that there is even one that is Turing-complete? Amidst the unruly chaos of Rule 30’s pseudorandom number generation and the ordered austerity of Rule 90’s perfect Sierpinski triangles, what deep mathematical forces conspired to give us this – this simple rule which, by itself alone, is capable of just enough complex behavior to be capable of carrying out computations? It balances on the knife’s edge between the dynamic and the static, exhibiting a kind of critical behavior of the sort that can also be seen in discussions of neuroscience and the physics of phase transitions.

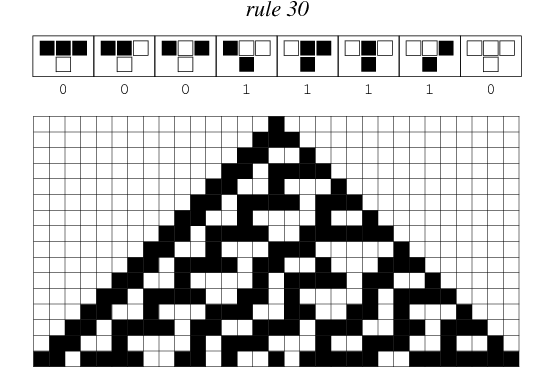
Rule 30, sometimes used as a pseudorandom number generator

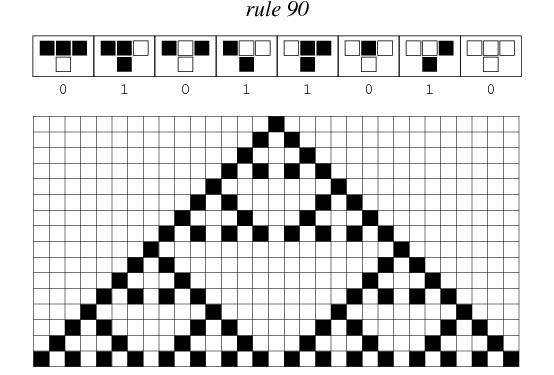
Rule 90, which generates Sierpinski triangles when initialized with a single pixel

The scarf also serves for me as a physical symbol of the following cluster of philosophical problems: What ethics govern the simulation of minds? If I were to create a scarf with a simulation of a mind in a video game environment (such as the one in The Talos Principle), is it at all meaningful – ethically – for me to sit there and knit out the entire scarf so that the simulation’s output is legible to us, or is it equally meaningful for me to merely cast on the start state of the scarf, and note how I might allow the computation to proceed if I were to knit out the entire scarf? If the two situations are the same, is it also equally meaningful for me to merely think about creating the scarf, designing its start state in my head, but never casting it onto physical yarn? And if the full spectrum of situations are not the same, then why?

I used YouTube videos to learn the technique of double-knitting in order to be able to construct a scarf with a two-color pixelated pattern. Due to the double-knitting constraint, the pixels on one side of the scarf are inverted on the other side, so technically it’s a scarf bearing Rule 110 on one side and Rule 193 on the other.

Rule 105 Scarf

Unlike the rule 110 scarf, this knitting project is my current work in progress.

The premise: Let’s say you want to create a Möbius strip scarf… but you also want it to be a cellular automaton.

Simply diving in to knitting any old cellular automaton won’t do, because in order to make it be Möbius, you must flip it around and join it to itself as the end of the process. For example, I clearly cannot do this with my rule 110 scarf. As shown, the final row does not proceed smoothly into the starting row, as would have been required!

What’s more, even deeper than this requirement about the final row’s behavior is the requirement that the whole cellular automaton rule must continue to be the same, even when we flip the scarf around. As we can see in the above example, leftward-leaning white triangles on blue (Rule 110) is a completely different pattern texture from rightward-leaning blue triangles on white (Rule 193).

This imposes the following two constraints on any cellular automaton we choose to Möbiusify:

1. The rule must be left-right symmetric.
2. The rule must be zero-one symmetric.

Alternatively put, using Wolfram’s terminology, the rule must be equal to its mirrored complement.

This requirement limits us to a small handful of valid rules, many of which are so simple as to be blindingly, boringly unaesthetic. (Rule 51 is one example of a blindingly boring rule, not that I have any problem with stripes.)

I decided to choose Rule 105 for its aesthetics. Rule 150 is another nice one that I considered.

I also needed to choose how to deal with the boundary conditions. I decided to treat the edges as if the scarf wraps around on itself. In a certain sense, this makes it perhaps more like a Klein bottle than a Möbius strip, spiritually if not literally.

Given all of the above parameters, the only thing that remained to do was to find a starting state that produces a pattern that repeats on itself in an interesting, pretty way. Most starting states only repeat on themselves after a small number of timesteps – boring! I wanted to maximize the cycle length of my scarf, for maximum aesthetic appeal.

I sent over all of the above parameters to Anders as a small puzzle, and three lines of Mathematica later, received a characterization of the complete 22-dimensional optimal solution space on scarves of 38 columns, from which I chose the following start state. Using this start state, the pixels at row 511 are exactly what they need to be such that the row at 512 is a left-right-flipped and zero-one-flipped copy of row 1 – the mirrored complement!

Row 1 and the first several rows.

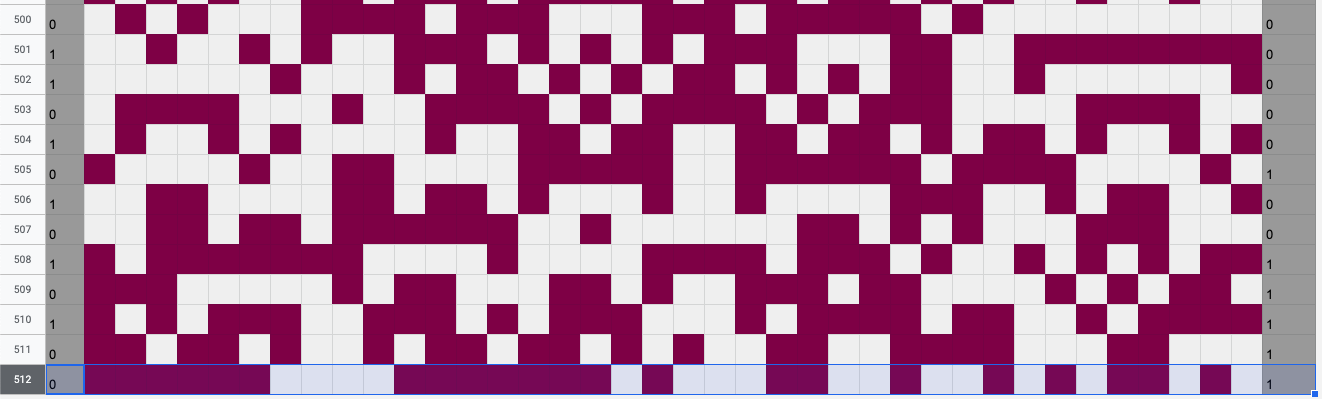
Row 512 is the mirrored complement of row 1.

I’m practicing the provisional cast-on knitting technique in order to make sure that once I reach row 511, I will be able to seamlessly knit the scarf to itself with nobody the wiser about where the scarf ever began or ended. That’s the red yarn in the below picture.

Right now I’m around 30 rows in. It’s going to be a long one!

I was inspired to start knitting by some friends who use knitting as a way to keep their hands busy while still attending to verbal inputs, such as having conversations or listening to others. The knitting projects themselves were inspired by the work of Fabienne Serriere (KnitYak), who creates scarves with cellular automata and other beautiful mathematical patterns using her industrial knitting machine. (She’s even got some of Rule 110 and Rule 105!)

Future work

Once I finish the Möbius strip scarf, the ultimate knitting project for me would be to create another Rule 110 project and have it actually encode a real Turing machine this time, unpacking the lessons from Cook’s proof of Rule 110’s Turing completeness in order to do so. I would pick a small Turing machine, convert it to a universal cyclic tag system using the polynomial reduction of Neary and Woods (2006), and then convert that into a Rule 110 start state.

A Concrete View of Rule 110 Computation (Cook 2009) demonstrates by example how to perform these reductions in order to compile a Turing machine into a Rule 110 cellular automaton. The resulting pattern would be wide enough that it would need be a blanket instead of a scarf!

If I wanted to truly satisfy my artistic preferences over such a project, I’d make sure to pick a Turing machine that’s a nice meaningful one. It’s too bad that A Relatively Small Turing Machine Whose Behavior Is Independent of Set Theory (Aaronson and Yedidia 2016) has 7,918 states, otherwise I would love to encode it!

The best-known five-state Busy Beaver Turing machine might be a nice, simple Turing machine to use for such a project. The best candidate currently known for BB(5) takes 47,176,870 steps before finally halting.

State transitions for a candidate BB(5), as given in Attacking the Busy Beaver 5.

A space-time history of the activity of Rule 110, started at the top with a row of randomly set cells, from Universality in Cellular Automata. Perhaps you see now what I mean by “blanket”.

Pilot, the startup I work at, announced our Series B today.

This is really exciting for me. I’ve been here for a little over a year and a half now. I joined right before the Series A, and since then we’ve outgrown offices twice and hired to more than 4x what our size was when I joined. This funding round raises our valuation to $355M (!) and also includes a strategic investment from Stripe, aligning their interests with ours (!!).

I joined Pilot in order to learn more stuff about engineering and also to learn more stuff about organizational efficiency and effectiveness, and I’ve been really satisfied on both fronts. Right after I joined I sometimes described the decision to friends as “Well, this is the founders’ third startup together, and their first two were successful exits, so… [eyebrow wiggle suggesting probable future success].” Waseem, Jessica, and Jeff really do know what they’re doing, and I haven’t been disappointed.

Optimize processes, not just tech

At Pilot I’ve learned a bunch about the optimization of human-centered processes and why it’s important. As someone who came from a hard computer science background, this lesson is one that I’ve only really absorbed during the last year or two, and it came both from observing Pilot and from observing other highly functional institutions within my broader community.

Pilot works on making bookkeeping less painful for humans to do, so that we can provide it at scale. This means not only that the engineering team’s automation tools have to be really good, but also that our human-centered processes for onboarding new team members and for spreading knowledge around have to be really good. As Catherine Olsson summarized my own description to me the other day, Pilot is “actually in the process optimization business.”

Checklists, common knowledge generation, and open lines of interpersonal communication – these and other tools are all really important to designing well-functioning processes for organizations made out of people.

Aim at real problems, and propagate incentives

I’ve also learned that the powerful engine of process optimization absolutely must be aimed at real problems in the world. I think this is a crucial puzzle piece that distinguishes startups that succeed from startups that don’t. I’ve liked getting to observe how the real-world problems faced by Pilot’s clients get propagated all the way down to the level of engineers’ day to day efforts.

Our organization is actually set up such that the incentives are really well aligned throughout. Potential clients (the source of real-world problems) come in via the sales team. Fulfilling our service to our clients becomes the problem of our operations team, who is tasked with closing the books. We record metrics about what’s taking our operations team the most time, as well as free-form feedback, and then the product team distills that data into goals for engineering and design.

The entire product process is legible and transparent to people on the engineering team, so I can audit what I’m working on and why, and question decisions at the appropriate level if I feel something’s off. Team members are also empowered to propose product directions directly.

If anything, the one thing I’d worry about with our setup is a hypothetical world where the most stress to deliver our service to our clients is felt by the operations team, and where the engineering team doesn’t feel the fire as much as the operations team does. We have been addressing this by specifying specific goals for the engineering team to meet in order to properly support the operations team, so I can trust that we will succeed inasmuch as we craft those goals carefully. And since we’re using data and metrics to motivate our choices, plus the management team sometimes ends up doing a little bookkeeping if we find ourselves under-capacity, I can trust that the organization’s incentives are aligned to craft those goals well.

Culture can be engineered

I’ve learned by example what it looks like for a community to deliberately engineer itself to have a good culture. On day 1, I was impressed when Jessica replied to a member of the team pointing out something to fix about part of our infrastructure by responding with “Good callout,” encouraging honest feedback. Just last month, a member of the engineering team took on the task of writing up a doc about our code review standards, making implicit social norms explicit. From various other members of the team I’ve learned about blameless retrospectives, about the New York Times rule, and about two kinds of feedback.

Pilot also has some employees with roots in the Recurse Center, whose social rules and attention to inclusiveness are another example of an organization achieving a well-engineered culture.

While we don’t currently have an explicit set of company values, as an individual participant in company culture I can tell from everyday communications that we think of ourselves as valuing work-life balance, diversity, and open communication, that we take actions that promote those values, and that we talk about those values often, thereby elevating them to common shared culture.

Short feedback loops can be engineered

Although I already knew that short feedback loops are important for getting good engineering velocity (write unit tests! use debugging tools!), one thing I’ve learned at Pilot is that it’s possible to structurally engineer an organizational system such that it has short feedback loops built in. In particular, our engineering team writes software for our in-house users, which means I have the luxury of not needing to regularly set up A/B tests in order to infer what’s going on in users’ minds; instead, we can ask our users directly.

Processes can become stale – change them

I’ve also seen firsthand that as organizations scale, the old processes and ways of doing things don’t necessarily work anymore and you have to find new ones. I’ve been pleased that as we’ve been growing, the management team has been attentive to whether there are any growing pains showing up in our processes, and I’ve been pleased that we’ve been actively working on moving to newer ways of doing things that work better for our current situation, rather than sticking with old solutions because they’re the way things have always been done.

Since I have joined, we have actively improved our systems for triaging issues, for tracking projects, and for conducting engineering team meetings, each time preventing ourselves from getting stuck in old ways that weren’t serving us as well anymore.

This seems like a pretty hard category of problem in general, and I’m interested in learning more heuristics for how to notice it and address it. It seems that as organizations grow larger, oftentimes problems like this can slip through the cracks.

Conclusions

There are countless other things I’ve learned that I could mention as well. I’ve learned a lot of stuff about good habits for frontend development in Vue.js from Pilot’s first engineer. I’ve learned what good management feels like as an employee from our engineering manager’s care and diligence. I’ve learned new things about computer security directly from the founder of the Twisted project, including how SSL certificate issuance works and how to do formal threat modeling.

Overall, I’ve been really interested in institutioncraft lately, and Pilot feels like a success case in institutioncraft from which I’ve learned a whole bunch. Of course, the things I’ve learned so far, like all things I learn, are a work in progress that is continued every day. I’m looking forward to building more stuff with these amazing people and to learning more as we grow together.

If you’ve seen my other posts, you probably already know that I am a sucker for good visual notations. Some of my favorites include circuitry for lambda calculus and Feynman diagrams.

So when I heard about a graphical notation for linear algebra, I really wanted to learn how it works. I decided to learn enough about Graphical Linear Algebra to be able to use the notation to express and solve one of my favorite puzzles from quantum computing. I was curious whether graphical linear algebra would make the problem more intuitive, and I think the notation actually succeeds!

In this post, I’ll pose the puzzle, along with some relevant background about logic gates in reversible computing. In a future post, I’ll give the puzzle’s solution, both with and without the aid of graphical linear algebra.

Reversible computing

We usually think of quantum computing (as exemplified by quantum circuits) as being more powerful than classical computing (as exemplified by the Turing machine), because it operates over qubits and qubits can exist in superposition, unlike normal bits. However, it’s also true that programs written for quantum computers must obey some constraints that programs written for Turing machines need not obey! In particular, all operations in a quantum circuit must be reversible.

For example, the classical XOR gate consumes two inputs and produces a value that’s true if and only if the two inputs are different. XOR is an example of an irreversible operation; knowing the value of A XOR B does not always give you enough information to derive what the values of the two inputs had been beforehand. An XOR gate has no inverse.

In contrast, the quantum equivalent of an XOR gate must produce at least one more output bit in order to preserve reversibility. Not only that, it must also use that output bit in a way that ensures that the two outputs could in principle be reversed in order to recover the original two inputs. The CNOT gate is one way of implementing these constraints in order to create a component that can be used to calculate XOR.

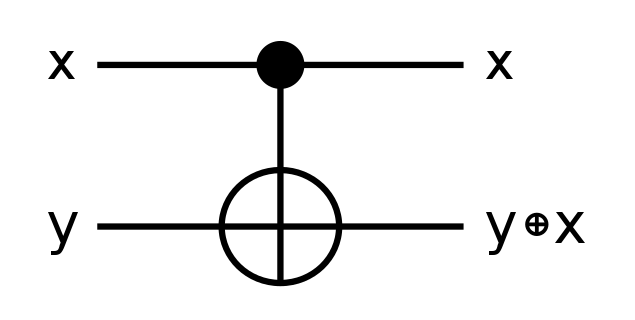
Unlike XOR, a CNOT gate has a logic gate that acts as its inverse. (All reversible gates must.)

The requirement for reversibility in quantum computing is, incidentally, an unavoidable consequence of the fact that the laws of physics require that information be conserved. In quantum physics, this concept is known as unitarity.

For more on this subject, I recommend Scott Aaronson’s excellent book Quantum Computing Since Democritus for a tour of the theory behind both classical and quantum computing. I also recommend the paper The Classification of Reversible Bit Operations by Aaronson, Grier, and Schaeffer if you want to learn more about logic gates in reversible computing.

Tangent. Real-world computers, like quantum computers (but unlike Turing machines), are actually built out of real physical stuff and must also use only reversible operations, because they work under the same laws of physics as quantum computers. Hidden under all of our careful abstractions, there are still trash bits and there is still physical entropy at play. It’s just that we programmers typically prefer to elide over those details and ignore them when thinking about algorithm design.

The details are still there, though; for example, it’s not possible to wipe a laptop’s hard drive, overwriting all of its data as 0s, without the entropy from that information being radiated out as some small amount of heat to the rest of the universe outside the laptop. This is a consequence of Landauer’s principle, first described by Rolf Landauer in a 1961 paper, Irreversibility and Heat Generation in the Computing Process. I would love to know more about the implications of Landauer’s principle on the energy efficiency of various algorithms when reversibility and entropy are taken into account – what low-hanging fruit are algorithm designers missing out on? – but haven’t yet found any good source material that combines the physics concepts with the theoretical computer science.

The puzzle

Consider the Fredkin gate, also known as CSWAP, a reversible gate which swaps bits 2 and 3 (below) only when bit 1 is true.

Consider also the Toffoli gate, also known as CCNOT, a reversible gate which inverts bit 3 if and only if bits 1 and 2 are both true.

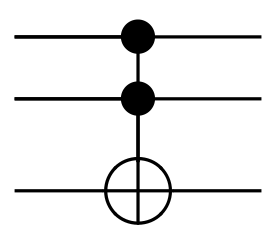
Note that Toffoli gates are complete gates in reversible computing: that is, it’s possible to form any other reversible logic operation using only some combination of Toffoli gates. This sort of completeness is the same completeness that NAND has for Boolean logic.

(The Toffoli gate does not by itself form a complete gate set in quantum computing, but it does when it’s combined with only one other gate, the Hadamard gate. Here’s one proof of that fact.)

The puzzle: Construct a Fredkin gate using only Toffoli gates.

Last April, I attended GaryConf WATCON Deconstruct 2017, got to listen to some excellent speakers, and enjoyed the opportunity to give a talk of my own: Programming Languages as Notations. Here are the slides.

When I was deciding what to talk about, I had been reading a bunch about the history of notations in math and physics. It’s really fascinating how different people throughout history have designed different languages for representing fundamentally identical concepts – for example, we have different notations for arithmetic, different notations for solving problems in quantum electrodynamics, and different notations for manipulating vectors. Some thoughts on each of these I’d like to share:

• Arithmetic: Compare Western civilization’s arithmetic notation and algorithms (for addition, multiplication, division, and fractions) to the notation and algorithms used in Ancient Egyptian mathematics. I didn’t end up mentioning Ancient Egyptian arithmetic in my talk, but it’s neat. Count Like An Egyptian by David Reimer is a fun resource for learning more.

• Quantum electrodynamics: Although two techniques – brute-force algebra and Feynman diagrams – each target the same kinds of problem (quantum electrodynamics calculations), Feynman diagrams are an interesting innovation both because they create both a new abstraction for dealing with those problems at a higher level and because they represent that abstraction in a beautifully visual way. Read David Kaiser’s article Physics and Feynman’s Diagrams for some neat history here, or check out his book Drawing Theories Apart for a more in-depth look. I love finding examples of mathematical notations that provide a new abstraction over the problems they solve, and I love highly visual notations, so Feynman diagrams really hit my aesthetic buttons.

• Vector notation is another example of a notation that creates a new abstraction: when we represent doubling some three-dimensional vector by writing down the notation 2x instead of 〈2x₁, 2x₂, 2x₃〉, for example, the vector abstraction has saved us from something that’s much like code duplication, and in the process has reduced the number of opportunities we have to accidentally introduce an error. Also, vector notation provides a hilarious example of Standardization Wars happening over one hundred years ago. Florian Cajori in his work A History of Mathematical Notation describes some of the vitriol that got thrown back and forth; some choice quotes from that book are in my slides. It’s nice to know (I suppose) that the modern impulse to fight over standards and their implementation details was shared by our ancestors as well.

Because notation had been on my mind, my talk centers around some parallels I see between mathematical notation design and programming language design.

One of those parallels: I like it when I find new programming paradigms that introduce new abstractions for the problems that we as programmers often solve. Here are some things in this general concept-space that have recently piqued my interest:

• Dafny is a research programming language that has syntax built in for writing down a function’s preconditions (requires) and postconditions (ensures); the verifier then checks that those conditions are true.
• Computational biology has a need for programming tools that model at many different levels of abstraction – from the molecular level (e.g. protein folding: tools – projects like Folding@Home and Foldit) to the cellular level (e.g. protein signalling networks: tools – programming languages like Kappa) to the whole-organism level (tools – we need them!).
• The pi-calculus is a model of computation in the same way that lambda calculus or Turing machines are models of computation, but is unusual in that it allows both parallel composition and sequential composition of code. Normally we write code sequentially, without the ability to specify when two operations or sequences of operations are independent and could very well have happened in parallel. Instead, the pi-calculus formalizes the ability to specify code as running sequentially or in parallel, opening up the possibility that the compiler could optimize code to run concurrently both more easily and with less thought required from the programmer. Pict is a concurrent programming language which is built upon the pi-calculus.

Another of those parallels: I like it when I find programming tools that enable visual representation of code. For example, snakefood is pretty nifty. Towards giving an example of what a completely visual programming language could look like, I discuss a visual circuitry-like notation I designed for lambda calculus, giving examples that dive into lambda calculus and combinatory logic. This blog post has more detail on that project. I don’t claim that we should be using visual representations all the time – user interface design is tricky, and our text-based systems have a lot going for them – but I think there still exist areas in which to innovate visually.